با داده‌ها چه می‌توان کرد؟ 5 - بررسی آماری

بررسی آماری Statistical Learning به مجموعه ابزاری گفته می شود که می تواند به درک و فهم ما نسبت داده های موجود یا جمع آوری شده کمک کند. در نظر کلی، این ابزار به دو دسته تحت نظارت Supervised و نظارت نشده Unsupervised تقسیم می شود.

بررسی آماری "تحت نظارت" به مدلهایی گفته می شود که بر اساس آن می شود یک روند را پیش بینی کرد و یا تخمین زد. از جمله حیطه کارکرد مدلهای آماری تحت نظارت می توان از کسب و کار Business، دارویی، سیاست، فیزیک کیهانی و بسیاری رشته های دیگر نام برد. مثلا در مورد رابطه میان دستمزد و تحصیلات افراد که از داده های چندین کمپانی در سالهای گذشته بدست آورده ایم، می توانیم از طریق مدلهای آماری پیش بینی کنیم که حقوق افرادی که طی سال آینده استخدام می شوند در چه حدودی خواهد بود. توجه کنیم که نتیجه و پیش بینی در این دسته بندی بصورت کمی (عددی) است.

در بررسی آماری نظارت نشده، ما بر نتیجه حاصله از تحلیل داده ها کنترلی نداریم و صرفا مشاهده کننده رابطه میان داده ها و دسته بندی های وارد شده در مدل آماری هستنم. در این دسته بندی، می توان در مورد داده های جمعیتی Demographic صحبت کنیم. ما امیدواریم که بتوانیم دریابیم که کدام یک از گروههای جمعیتی (از نظر نژاد، سطح درآمد و غیره) رفتار مشابه ای با گروههای دیگر مثلا در خرید اجناس از فروشگاههای خاص دارند و آنها را در گروه بندی خاص که به آن کلاستر Clustering، گفته می شود، قرار دهیم. در اینجا بر عکس قبلی، ما پیش بینی خاصی در مورد نتیجه نداریم.

 کلاستر Clustering

بررسی آماری تحت نظارت یا Supervised: برای روشن شدن بیشتر مقوله بررسی آماری در این دسته بندی، بهتر است که روی یک مثال مشخص کار کنیم. در نظر بگیرید که  یک کمپانی برای افزایش میزان فروش محصولاتش از چند نوع تبلیغ در رسانه های مختلف مانند تلوزیون، رادیو و روزنامه استفاده می کند. این کمپانی اطلاعات و داده های سال گذشته (یا سالهای گذشته) در زمینه اختصاص بودجه بطور جداگانه از طریق سه رسانه را در اختیار ما گذاشته و از ما راهنمایی می خواهد تا تعیین کنیم که آیا این تبلیغات در فروش محصولاتش تاثیر داشته؟ و اگر داشته کدامیک از این رسانه ها موثر تر بوده و به چه میزانی؟

اینها دقیقا سوالاتی است که علم داده ها از طریق بررسی آماری قادر به پاسخ است و تعیین می کند که اختصاص به کدام یک از این رسانه ها در میزان فروش، و تا به چه اندازه، موثر است. در اینجا بودجه اختصاصی را به مثابه متغیر ورودی و میزان فروش را به مثابه متغیر خروجی در نظر می گیریم. متغیرهای ورود (داده ها) را معمولا با X نشان می دهند. در این مثال بودجه تی وی X1، رادیو X2، و بودجه برای روزنامه را X3، در نظر می گیریم. با متغیرهای ورودی، پیش بینی کننده ها، متغیرهای مستقل هم گفته می شود.

فروش که به آن متغیر خروجی یا نتیجه (پاسخ) و یا متغیر وابسته گفته می شود را با متغیرY نشان می دهند.

عکس شماره 1- فروش (عمودی) در واحد هزار و متغیرها (افقی) در واحد هزار دلار نشان داده شده

ما حدس می زنیم که یک رابطه کمی quantitative بین فروش Y و متغیرهای X1, X2, X3 وجود دارد که می تواند با این معادله نشان داده شود:

Y = f(X) + Ɛ                                   معادله 1

f در اینجا یک تابع مشخص ولی ناشناخته از X1,...,Xp است و Ɛ اشتباه تصادفی است که از X مستقل است و حد وسط average آن صفر می باشد. در معادله بالا f معرف اطلاعات سیستماتیکی است که X در مورد Y به ما ارائه می دهد. در حقیقت بررسی آماری به شیوه هایی گفته می شود که می تواند f را تخمین بزند.

چرا می خواهیم f  را تخمین بزنیم. برای اینکه در بیشتر موارد داده ها X بوفور قابل دسترس است (بعنوان مثال در اینجا بودجه اختصاص یافته به رسانه ها را خود کمپانی در اختیار ما گذاشته) اما تخمین Y که همان فروش باشد براحتی امکانپذیر نیست. از آنجاییکه متوسط اشتباه را صفر در نظر گرفتیم، این معادله را می توانیم بنویسیم:

Ŷ = 𝑓ˆ(X)                                        معادله 2

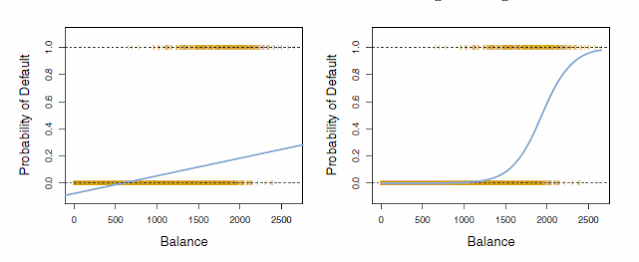
در این معادله Ŷ(کلاه دار)، تخمین ما از Y حقیقی و ˆf (کلاه دار) تخمینی از تابع واقعی است. با تخمین ˆf می توانیم Y کلاه دار که تخمینی از فروش است را بدست آوریم. در عکس شماره 1، شیب خط ممتدی که از میان داده ها عبور کرده است، همان ˆf ( کلاه دار) است که به ما نشان می دهد با افزایش چه میزان از X(بودجه تبلیغات یک رسانه)، مقدار Y(فروش) بالا می رود.

در اینجا امکان پیدایش دو نوع خطا وجود دارد. یکی ˆf  که تخمین است و امکان تفاوتش با f  همواره وجود دارد. این نوع خطا قابل جبران است که می توان آن را از طریق تکنیک های آماری کاهش داد، اصطلاحا Reducible می خوانند.

نوع دیگر خطا ناشی از Ɛ است. همانطور که گفته شد، این خطا مستقل از X است و از آنجاییکه در متغیرها لحاظ نمی شود و نقشی ندارد، قابل جبران نبوده و اصطلاحا Irreducible خوانده می شود.

بهتر است برای فهم دقیق خطاهای ذکر شده در بالا فعلا انرژی گذاری بسیار نکنید. همانطور که قبلا هم بارها تاکید کردم، هدف ما اینجا نه یادگیری کامل زبان پایتون برای نوشتن اپلیکیشن های پیچیده است و نه در مورد بررسی های آماری، اثبات فرمولهای مختلف ریاضی و آماری است. یکی از دلایلی که بسیاری از افراد در ابتدا و یا میانه راه، کلا قید یادگیری این رشته بسیار جالب و فکری را می زنند، درگیر شدن بیش از حد در پیچیدگی های غیر ضرروی و تکنیکی است.

پس از آنکه توانستید اولین سری داده ها را جمع و جور کنید و بر روی آنها حداقل الگوریتم آماری را از طریق نرم افزار پانداز یا آر اجرا کنید و در پایان رابطه داده ها و تاثیر آنها بر Y را تحلیل کنید، می توانید بیشتر وارد ریز قضایا بشوید (و باید هم بیشتر یاد بگیرید). اما تا آنزمان سعی می کنم که موضوعات را پیچیده نکنم. 

این بحث را در قسمت آینده ادامه می داهیم.

- اطلاعات مربوط به این بخش و قسمتهای آینده در باره پانداز، بیشتر برگفته از کتاب  Python for Data Analysis, Data Wrangling with Pandas, NumPy,and IPython چاپ دوم از انتشارات اورایلی است که توسط Wes McKinney، خالق پانداز، نوشته شده است. 

*- بیشتر ملاتها در مورد بررسی آماری در این سلسله مطالب، برگرفته از دو کتاب An Introduction to Statistical Learning و The Elements of Statistical Learning Data Mining, Inference, and Prediction از انتشارات سپرینگر springer.com/us و کلاسهای ارائه شده آنلاین توسط دانشگاه هاروارد است.

**- استفاده از این سلسله مطالب با ذکر منبع آزاد است.